0.개요
앞서, Support Vector Machine은 다음과 같은 제약식이 있는 최적화 문제를 라그랑주 문제로 풀었다.
$$\text {max}\quad L_D(\alpha_i)=\sum^n_{i=1}\alpha_i - \frac {1}{2}\sum^n_{i=1}\sum^n_{j=1}\alpha_{i}\alpha_{j} y_i y_j x^{T}_ix_j$$
$$\text {subject to} \quad \sum^n_{i=1}\alpha_i y_i = 0, \ 0 \leq \alpha_i \leq C, \quad i = 1, \dots , n $$
그러나 분류모델로 선형 SVM을 가정했을 때 soft margin을 사용해 어느 정도 오분류를 허용하더라도 다음과 같은 input space에서 데이터를 정확하게 분류하는 초평면을 찾기는 쉽지 않다. 그러면 input space에 있는 비선형 특징을 가진 데이터를 선형 특징을 가지는 고차원 space에 뿌려주면 선형으로 분리 가능하지 않을까?

1.예시: 높은 차원으로 매핑하는 함수(basis function)
예를 들어, 다음과 같은 선으로 이루어져 있는 비선형 특징을 가지는 1차원 데이터는 선형으로 분류하기 힘들다.


그때 비선형 input space를 선형 특징을 가지도록 Φ(X) = (X, X^2) 기저함수를 이용하여 2차원 feature space로 1차원 데이터를 mapping하면 다음과 같이 선형 분류 가능한 feature space가 생성된다.

2차 원상 데이터에서도 마찬가지다. 다음과 같은 2차원 input space의 데이터는 선형분리가 불가능하다.
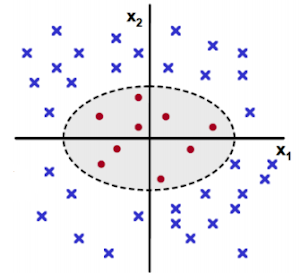

2차 원상 데이터를 다음과 같은 매핑 함수를 이용해 3차원 공간으로 뿌려줄 수 있다. 그러면 다음과 같이 새로운 축을 기반으로 데이터를 분류하는 초평면을 찾을 수 있다.

어떠한 고차원으로 비선형 특징을 가진 데이터를 뿌려서 선형으로 분리할 수 있는 mapping 함수를 찾는다면 SVM 목적식에 다음과 같은 mapping 함수를 적용해 선형분리 가능한 초평면을 찾을 수 있다.
$$\text {max}\quad L_D(\alpha_i)=\sum^n_{i=1}\alpha_i - \frac {1}{2}\sum^n_{i=1}\sum^n_{j=1}\alpha_{i}\alpha_{j} y_i y_j \Phi{(x_i)}^{T}\Phi{(x_j)}$$
2.basis function의 내적 연산량을 kernel 사용으로 효율적으로 만들어 보자
그러나 1) $\Phi{(x)}$ 고차원 mapping 함수를 정의하는 것과 2) $\Phi{(x_i)}^{T}\Phi{(x_j)}$의 고차원 mapping 연산량 + 내적 연산은 연산량 측면에서 굉장히 비효율적이다. 이 문제를 해결하는 것이 kernel이다. 이미 증명된 다음과 같은 kernel을 사용하면 우리는 $\Phi$ 함수가 어떤 함수인지 몰라도 된다. 그리고 $\Phi$ 함수의 내적 계산을 kernel이 해주기 때문에 연산량 측면에서 효율적이다. 그 대신 kernel은 Mercer's Theorem을 만족해야 한다.
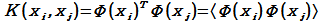

- Kernel 함수 K 가 실수 scalar 를 출력하는 continuous function일 때,
- Kernel 함수값으로 만든 행렬이 Symmetric(대칭행렬)이고,
- Positive semi-definite(대각원소>0)라면,
- K(xi, xj) = K(xj, xi) = <Φ(xi), Φ(xj)>를 만족하는 mapping Φ 가 존재한다.
= Reproducing kernel Hilbert space
위 Mercer's Theorem을 만족하는 증명된 Kernel function은 아래와 같이 다양하게 존재한다. 그리고 이 kernel을 이용하는 것을 kernel trick이라 한다.

따라서 kernel trick을 적용한 svm 목적식은 다음과 같으며 비선형 문제에서도 kernel을 이용해 svm의 목적인 데이터를 선형적으로 분류하는 초평면을 효율적으로 찾을 수 있다.
$$\text {max}\quad L_D(\alpha_i)=\sum^n_{i=1}\alpha_i - \frac {1}{2}\sum^n_{i=1}\sum^n_{j=1}\alpha_{i}\alpha_{j} y_i y_j K(x_i, x_j)$$

그러나 실제 데이터에서 비선형 특성을 띄는 경우가 많아 나는 가우스 kernel을 주로 사용하지만 linear kernel을 실험적으로 같이 사용하는 것이 권장되고 (Hastie, 2001)에 따르면 고차원(high dimensional) 데이터의 경우에는 복잡한 비선형 kernel 보다는 linear kernel이 더 나은 성능을 보일 것으로 생각된다. 그리고 kernel의 경우 $\Phi$ 함수를 계산할 필요가 없어 non-parametric 한 특징을 가지고 있고, 기하학적인 형태로는 두 벡터의 내적(inner product)으로 cosine 유사도를 의미해 similarity 함수라고도 불린다.
4.reference
https://sonsnotation.blogspot.com/2020/11/11-1-kernel.html
[머신러닝/딥러닝] 11-1. Kernel의 이해와 종류
sonsnotation.blogspot.com
Hastie, T., Tibshirani, R. and Friedman, J. H. (2001). The Elements of Statistical Learning, 2nd Ed., Springer, New York
'Data Science > 머신러닝' 카테고리의 다른 글
| [PySpark] 신용카드 사기거래 탐지 모델링(2) - 성능지표정의 (0) | 2023.06.22 |
|---|---|
| [PySpark] 신용카드 사기거래 탐지 모델링(1) - 데이터 탐색 (0) | 2023.06.21 |
| [머신러닝] 분류모델 성능지표 - 혼동행렬, AUC-ROC 커브, Lift/gain 차트 (1) | 2023.03.09 |
| [머신러닝] Random Forest, XGBoost, LightGBM 비교 (1) | 2023.01.03 |
| [머신러닝]Support Vector Machine(SVM)에 대해 알아보자 (0) | 2022.11.27 |