0.History
서포트 벡터 머신(support vector machine; svm) 알고리즘은 Vapnik, Chervonenkis(1963)에 의해 고안됐다. 1992년 커널 트릭(kernel trick) 방법론을 적용해 마진(margin)을 최대화하는 초평면(hyperplane)을 찾는 비선형 분류기로 확장했으며, 1995년에는 소프트 마진(sorft margin) 개념을 도입해 svm의 분류기의 성능을 높였다.
1.SVM - 초평면(hyperplane), 마진(margin)
우선, 여기서 svm은 지도학습 분류기로 이진 분류만 고려하기로 한다.
주어진 훈련데이터(training observation)를 이용하여 마진(margin)을 최대화하는 초평면(hyperplane)을 찾는 분류기이다.
$$\text {입력 공간:} \quad \mathcal {X} = \Pi_{j=1}^{p}\mathcal {X_j} \subset \mathbb {R}^p$$
$$\text {출력 공간:} \quad \mathcal {Y} \in \lbrace -1,+1 \rbrace $$
$$\text {훈련 데이터:} \quad (x_i, y_i) \in \mathcal {X} \times \mathcal {Y}, \quad i = 1, \dots, n $$
여기서 초평면은 subspace whose dimension is one less than that of its ambient space. 즉, n차원의 공간에서 n-1차원의 부분 공간이 된다. 예를 들어, 2차원의 공간에서 1차원의 선이 초평면이 되고, 3차원의 공간에서 2차원의 면이 초평면이 된다. 따라서 svm은 부모 공간을 두 개의 공간으로 나누는 적절한 초평면을 찾음으로써 데이터를 분류하게 된다.
마진(margin) 은 분리하는 초평면으로부터 훈련 데이터까지의 수직거리를 계산하여 가장 작은 거리를 나타내며 svm은 이러한 마진이 가장 큰 초평면을 찾아 실험 데이터에 적용한다.
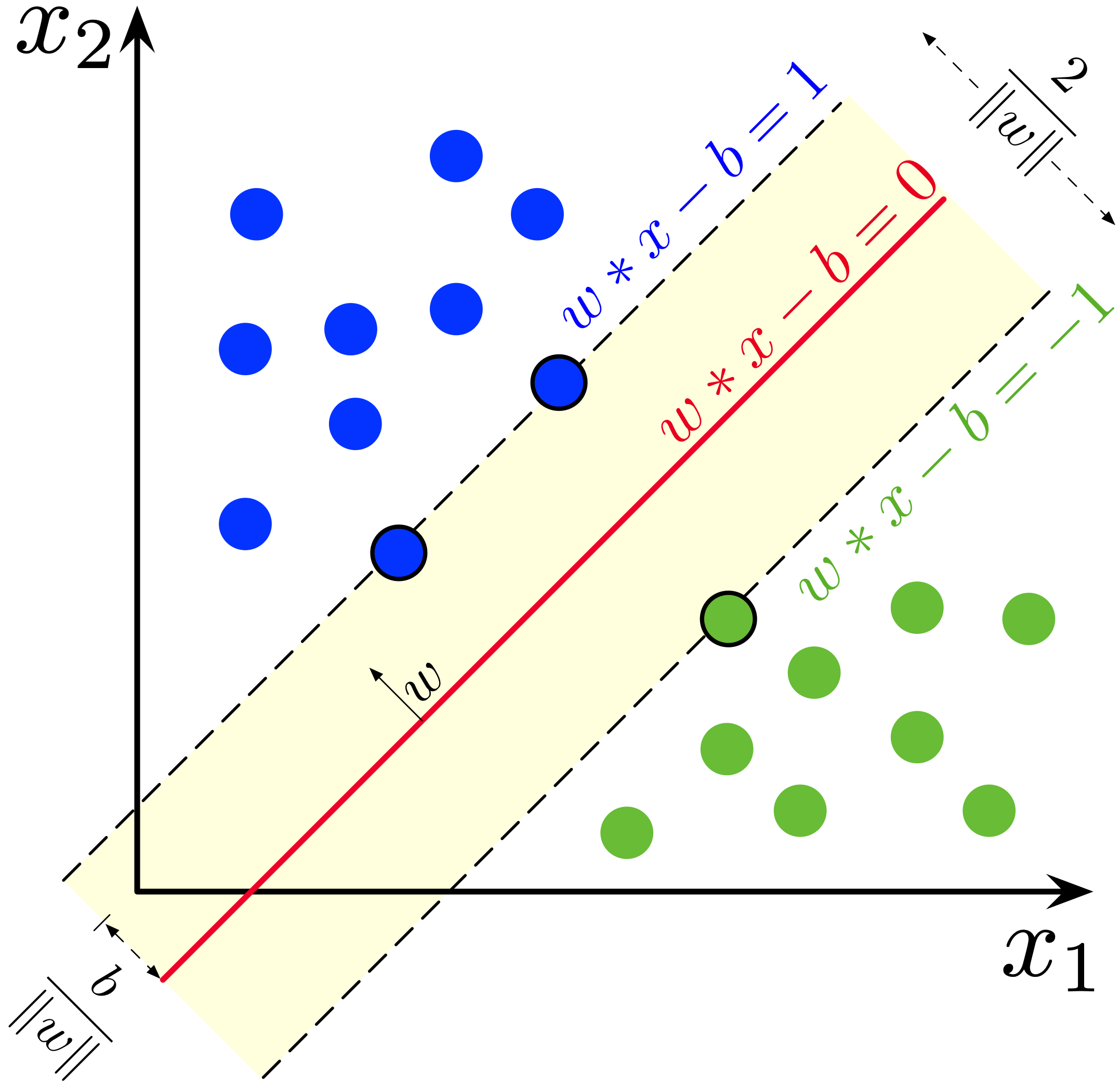
따라서, 위키의 그림 예처럼 2차원 공간상에서 선형적으로 분리가 되는 경우 다음과 같은 초평면을 찾게 된다. 여기서 $w$는 초평면의 법 선 벡터(norm vector)이다.
$$w^Tx_i - b = 0 $$
$$w^Tx_i - b \geq 1, \quad if \quad y_i = 1$$
$$w^Tx_i - b \leq -1, \quad if \quad y_i = -1$$
초평면 사이에 데이터가 없다는 제약조건을 추가하고, 두 서포트 벡터 사이의 거리 $ \frac {2}{||w||}$ 즉, 마진을 최대화하는 최적화 문제를 풀게 되는데, 다음과 같이 동등한 최적화 문제를 풀게 된다.
$$ \text {min}_{w, b}\frac {||w||^2}{2}$$
$$ \text {subject to} \ y_{i}(w^Tx_i - b) \geq 1$$
$$ \text {for} \ i = 1, \dots , n $$
1995년 Cortes와 Vapnik은 어느 정도의 오분류율을 허용하는 경첩 손실(hinge loss)을 도입하여 기존의 svm을 확장했다.
$$ \min_{w, b} \quad \frac {||w||^2}{2} + C\sum^n_{i=1}[1-y_i(w^{t} x_i + b)]_{+} $$
여기서, $[1-u]_{+} = max(0, 1-u)$ 경첩 손실로 미분 불가능한 형태이다.
2.SVM - 최적화 문제
앞서 구한 경첩 손실은 미분이 불가능하기 때문에 $\xi_i$(slack variable)를 도입하면 다음과 같은 최적화 식을 풀게 된다.
$$ \min_{w, b,\xi} \quad \frac {||w||^2}{2} + C\sum^n_{i=1}\xi_i $$
$$ \text {subject to} \ y_{i}(w^Tx_i - b) \geq 1 - \xi_i, \quad \xi_i \geq 0$$
$$ \text {for} \ i = 1, \dots , n $$
로 나타낼 수 있는데 위의 목적 함수는 마진을 크게 하는 것과 에러에 대한 페널티를 작게 하는 것의 균형을 맞추게 되며 어느 정도의 오분류를 허용하는 방법이다.
제약조건이 있는 최적화 식은 라그랑주 승수법을 이용하면 구할 수 있다. 제약 조건에 라그랑주 승수(Lagrange multiple)를 도입하여
$$\text {min} \quad L_p(w, b,\xi_{i},\alpha_i,\mu_i) = \frac {||w||^2 }{2} + C\sum^n_{i=1}\xi_i - \sum^n_{i=1}\alpha_{i} y_i[(w^{T} x_i+b)-(1-\xi_i)]- \sum^n_{i=1}\mu_i\xi_i$$
$$\text {subject to} \ \alpha_i \geq 0, \quad \mu_i \geq 0, \quad i = 1, 2,..., n$$
다음과 같은 라그랑주 프라이멀(Lagrange Primal) 함수를 풀게 되는데 KKT조건(Karush - Kuhn - Tucker conditions)에서는 $L_p$를 $w, b, \xi_i$로 편미분 한 식이 0이 되는 지점에서 최솟값을 가지게 된다.
$$\frac {\partial L_p}{\partial w} = 0\ \rightarrow \ w = \sum^n_{i=1}\alpha_i y_i x_i$$
$$\frac{\partial L_p}{\partial b} = 0\ \rightarrow \ \sum^n_{i=1}\alpha_i y_i = 0$$
$$\frac{\partial L_p}{\partial \xi_i} = 0\ \rightarrow \ C - \alpha_i - \mu_i = 0$$
볼록 함수(convex function)이고 KKT조건을 만족하면 쌍대 함수(Dual function)를 구할 수 있다. 따라서, 위의 편미분 한 식을 $L_p$에 대입하면
$$\text {max}\quad L_D(\alpha_i)=\sum^n_{i=1}\alpha_i - \frac {1}{2}\sum^n_{i=1}\sum^n_{j=1}\alpha_{i}\alpha_{j} y_i y_j x^{T}_ix_j$$
$$\text {subject to} \quad \sum^n_{i=1}\alpha_i y_i = 0, \ 0 \leq \alpha_i \leq C, \quad i = 1, \dots , n $$
쌍대 문제(Dual problem)를 구할 수 있는데 결국 $\alpha_i$에 관한 2차 계획법 문제(quadratic programming)이며 공통 최적 값은 다음과 같다.
$$w^* = \sum^n_{i=1}\alpha^*_i y_i x_i$$
듀얼 문제로 풀게 되면 상수 C가 오직 라그랑주 승수 법의 $\alpha$ 제약조건에 등장함으로써, 슬랙 변수($\xi_i$)가 사라진다는 점이다. 위의 공식화와 이것이 실제 상황에서 미치는 큰 영향에 대해서 Cortest와 Vapnik은 2008년에 ACM Paris Kanellakis Award를 수상했다고 한다.
다음 article로는 1992년 제안된 svm의 최대 마진 초평면 문제에서 커널 트릭(kernel trick)을 적용해 비선형 문제로 확장한 kernel 함수에 대해서 알아보자.
3.reference
https://mathworld.wolfram.com/Hyperplane.html
https://en.wikipedia.org/wiki/Support_vector_machine
https://en.wikipedia.org/wiki/Hyperplane
'Data Science > 머신러닝' 카테고리의 다른 글
| [PySpark] 신용카드 사기거래 탐지 모델링(2) - 성능지표정의 (0) | 2023.06.22 |
|---|---|
| [PySpark] 신용카드 사기거래 탐지 모델링(1) - 데이터 탐색 (0) | 2023.06.21 |
| [머신러닝] 분류모델 성능지표 - 혼동행렬, AUC-ROC 커브, Lift/gain 차트 (1) | 2023.03.09 |
| [머신러닝] Random Forest, XGBoost, LightGBM 비교 (1) | 2023.01.03 |
| [머신러닝] Kernel/Kernel trick(커널, 커널트릭) (0) | 2022.12.23 |